Should Camera Belong To Renderer Or Scene
Section v.ane
3.js Nuts
Three.js is an object-oriented JavaScript library for 3D graphics. Information technology is an open-source project created by Ricardo Cabello (who goes by the handle "mr.doob", https://mrdoob.com/), with contributions from other programmers. It seems to be the nigh popular open-source JavaScript library for 3D web applications. 3.js uses concepts that yous are already familiar with, such as geometric objects, transformations, lights, materials, textures, and cameras. Only information technology as well has additional features that build on the ability and flexibility of WegGL.
You tin download three.js and read the documentation at its primary web site, https://threejs.org. The download is quite large, since it includes many examples and back up files. In this book, I use Release 129 of the software, from June, 2021. Version 1.ii of this book used Release 89. In that location have been a number of significant changes in the API since that release, and many programs written for older releases will not run under Release 129. You should be aware that some of the material most three.js that yous might find on the Cyberspace does not apply to the almost recent version.
One of the changes in three.js is that it is at present written equally a "modular" JavaScript program. Modules are relatively independent components. A module only has admission to an identifier from some other module if the identifier is explicitly "exported" by one module and "imported" by the other. You lot volition come across modules used in many three.js examples, which include the appropriate input and consign commands. However, modules are not used in this textbook. Information technology is possible to build a non-modular Javascript program from modular source code, and it is the non-modular version of iii.js that is used in this textbook.
The core features of iii.js are divers in a unmarried large JavaScript file named "three.js", which can be plant in a build directory in the three.js download. This version is designed to be used with either modular or not-modular programs. There is too a smaller "minified" version, three.min.js, that contains the same definitions in a format that is not meant to be human-readable. To use three.js on a web page, yous tin can load either script with a <script> element on the page. For example, bold that three.min.js is in the aforementioned binder equally the web page, so the script element would exist:
<script src="3.min.js"></script>
In addition to this core, the three.js download has a directory containing many examples and a variety of back up files that are used in the examples. The examples employ many features that are not office of the three.js core. These add together-ons can exist found in a folder named js within the binder named examples in the download (or in a folder named jsm for the modular versions). Several of the add-ons are used in this textbook.
Copies of three.js, 3.min.js, and several add-on scripts tin can exist institute in the threejs folder in the source binder of this textbook's web site. The three.js license allows these files to be freely redistributed. Simply if you plan to do any serious work with three.js, yous should read the documentation on its web site virtually how to utilise it and how to deploy information technology.
5.1.1 Scene, Renderer, Photographic camera
Three.js works with the HTML <canvas> element, the aforementioned affair that we used for second graphics in Section 2.half-dozen. In virtually all web browsers, in addition to its 2nd Graphics API, a canvas too supports drawing in 3D using WebGL, which is used by three.js and which is nigh as unlike as it can exist from the 2nd API.
3.js is an object-oriented scene graph API. (See Subsection two.4.ii.) The bones procedure is to build a scene graph out of 3.js objects, and and so to render an image of the scene it represents. Animation tin can be implemented past modifying backdrop of the scene graph between frames.
The 3.js library is fabricated upwards of a large number of classes. 3 of the most basic are 3.Scene, THREE.Camera, and Iii.WebGLRenderer. (There are actually several renderer classes available. 3.WebGLRenderer is by far the near mutual. It uses WebGL 2.0 if available, simply can besides use WebGL 1.0 if non. One culling is Three.WebGL1Renderer, with a "i" in the name, which forces the utilize of WebGL 1.0.) Athree.js program will need at least ane object of each type. Those objects are often stored in global variables
let scene, renderer, camera;
Note that almost all of the 3.js classes and constants that we will use are properties of an object named Three, and their names begin with "THREE.". I will sometimes refer to classes without using this prefix, and it is not ordinarily used in the three.js documentation, merely the prefix must always exist included in actual program lawmaking.
A Scene object is a holder for all the objects that make up a 3D world, including lights, graphical objects, and mayhap cameras. It acts as a root node for the scene graph. A Photographic camera is a special kind of object that represents a viewpoint from which an image of a 3D earth can be made. Information technology represents a combination of a viewing transformation and a projection. A WebGLRenderer is an object that tin create an image from a scene graph.
The scene is the simplest of the three objects. A scene tin be created as an object of type THREE.Scene using a constructor with no parameters:
scene = new Iii.Scene();
The function scene.add(particular) tin can be used to add cameras, lights, and graphical objects to the scene. Information technology is probably the but scene function that you will need to call. The role scene.remove(item), which removes an particular from the scene, is also occasionally useful.
There are two kinds of photographic camera, 1 using orthographic project and one using perspective projection. They are represented by classes Iii.OrthographicCamera and THREE.PerspectiveCamera, which are subclasses of THREE.Photographic camera. The constructors specify the projection, using parameters that are familiar from OpenGL (see Subsection 3.3.3):
photographic camera = new THREE.OrthographicCamera( left, right, elevation, lesser, about, far );
or
camera = new Three.PerspectiveCamera( fieldOfViewAngle, aspect, near, far );
The parameters for the orthographic photographic camera specify the ten, y, and z limits of the view volume, in eye coordinates—that is, in a coordinate system in which the camera is at (0,0,0) looking in the management of the negative z-centrality, with the y-centrality pointing upwardly in the view. The near and far parameters requite the z-limits in terms of distance from the camera. For an orthographic projection, most tin can be negative, putting the "near" clipping airplane in back of the photographic camera. The parameters are the same as for the OpenGL function glOrtho(), except for reversing the lodge of the two parameters that specify the summit and bottom clipping planes.
Perspective cameras are more than mutual. The parameters for the perspective photographic camera come from the part gluPerspective() in OpenGL's GLU library. The kickoff parameter determines the vertical extent of the view volume, given equally an angle measured in degrees. The aspect is the ratio between the horizontal and vertical extents; it should usually exist prepare to the width of the canvas divided by its height. And nearly and far give the z-limits on the view volume as distances from the photographic camera. For a perspective projection, both must be positive, with about less than far. Typical code for creating a perspective photographic camera would be:
camera = new THREE.PerspectiveCamera( 45, canvas.width/sail.height, 1, 100 );
where canvass holds a reference to the <canvas> element where the image will exist rendered. The near and far values mean that only things between one and 100 units in front of the camera are included in the image. Retrieve that using an unnecessarily large value for far or an unnecessarily small value for near can interfere with the accurateness of the depth test.
A camera, like other objects, tin can be added to a scene, but it does not have to be part of the scene graph to be used. You might add together it to the scene graph if you want it to be a parent or child of another object in the graph. In whatever case, you will generally want to apply a modeling transformation to the photographic camera to set its position and orientation in 3D space. I will comprehend that later when I talk nigh transformations more than generally.
A renderer is an instance of the grade THREE.WebGLRenderer (or THREE.WebGL1Renderer, which is used in exactly the same mode). Its constructor has one parameter, which is a JavaScript object containing settings that bear upon the renderer. The settings yous are well-nigh likely to specify are sheet, which tells the renderer where to draw, and antialias, which asks the renderer to use antialiasing if possible:
renderer = new THREE.WebGLRenderer( { canvas: theCanvas, antialias: truthful } ); Here, theCanvas would be a reference to the <sail> chemical element where the renderer will display the images that information technology produces. (Note that the technique of having a JavaScript object as a parameter is used in many three.js functions. It makes it possible to back up a big number of options without requiring a long list of parameters that must all be specified in some particular order. Instead, you but need to specify the options for which yous want to provide non-default values, and yous can specify those options by name, in any order.)
The main thing that you want to practise with a renderer is render an image. For that, you besides need a scene and a camera. To render an paradigm of a given scene from the bespeak of view of a given photographic camera, telephone call
renderer.return( scene, camera );
This is actually the fundamental command in any iii.js application.
(I should annotation that near of the examples that I accept seen practise not provide a sheet to the renderer; instead, they allow the renderer to create it. The canvas can so be obtained from the renderer and added to the folio. Furthermore, the canvass typically fills the entire browser window. The sample plan threejs/total-window.html shows how to do that. Notwithstanding, all of my other examples use an existing canvas, with the renderer constructor shown above.)
5.1.2 THREE.Object3D
A three.js scene graph is made up of objects of blazon THREE.Object3D (including objects that vest to subclasses of that course). Cameras, lights, and visible objects are all represented by subclasses of Object3D. In fact, Three.Scene itself is also a subclass of Object3D.
Whatever Object3D contains a list of child objects, which are also of type Object3D. The child lists define the construction of the scene graph. If node and object are of type Object3D, and so the method node.add(object) adds object to the list of children of node. The method node.remove(object) can be used to remove an object from the listing.
A iii.js scene graph must, in fact, exist a tree. That is, every node in the graph has a unique parent node, except for the root node, which has no parent. An Object3D, obj, has a belongings obj.parent that points to the parent of obj in the scene graph, if any. You should never prepare this property directly. It is ready automatically when the node is added to the kid listing of some other node. If obj already has a parent when it is added as a child of node, and so obj is first removed from the child listing of its electric current parent before it is added to the child list of node.
The children of an Object3D, obj, are stored in a holding named obj.children, which is an ordinary JavaScript assortment. However, y'all should always add and remove children of obj using the methods obj.add() and obj.remove().
To make it easy to duplicate parts of the structure of a scene graph, Object3D defines a clone() method. This method copies the node, including the recursive copying of the children of that node. This makes information technology easy to include multiple copies of the same structure in a scene graph:
permit node = Three.Object3D(); . . // Add together children to node. . scene.add(node); permit nodeCopy1 = node.clone(); . . // Alter nodeCopy1, maybe use a transformation. . scene.add(nodeCopy1) let nodeCopy2 = node.clone(); . . // Modify nodeCopy2, maybe employ a transformation. . scene.add(nodeCopy2);
An Object3D, obj, has an associated transformation, which is given past properties obj.scale, obj.rotation, and obj.position. These properties correspond a modeling transformation to be applied to the object and its children when the object is rendered. The object is first scaled, then rotated, then translated according to the values of these properties. (Transformations are really more than complicated than this, but we volition keep things simple for now and will return to the topic later.)
The values of obj.scale and obj.position are objects of blazon THREE.Vector3. AVector3 represents a vector or betoken in 3 dimensions. (At that place are similar classes THREE.Vector2 and 3.Vector4 for vectors in ii and 4 dimensions.) A Vector3 object can exist constructed from three numbers that give the coordinates of the vector:
let v = new THREE.Vector3( 17, -3.14159, 42 );
This object has properties v.x, v.y, and five.z representing the coordinates. The properties can be set up individually; for example: 5.x = 10. They tin as well be set up all at once, using the method v.prepare(x,y,z). The Vector3 grade also has many methods implementing vector operations such as addition, dot product, and cross product.
For an Object3D, the properties obj.scale.ten, obj.scale.y, and obj.scale.z requite the amount of scaling of the object in the 10, y, and z directions. The default values, of course, are 1. Calling
obj.scale.set up(ii,2,two);
means that the object volition be subjected to a compatible scaling factor of 2 when it is rendered. Setting
obj.calibration.y = 0.5;
will compress it to one-half-size in the y-direction only (assuming that obj.scale.10 and obj.scale.z still accept their default values).
Similarly, the properties obj.position.x, obj.position.y, and obj.position.z give the translation amounts that will be practical to the object in the x, y, and z directions when it is rendered. For example, since a camera is an Object3D, setting
camera.position.z = 20;
means that the camera volition be moved from its default position at the origin to the point (0,0,xx) on the positive z-axis. This modeling transformation on the camera becomes a viewing transformation when the camera is used to return a scene.
The object obj.rotation has backdrop obj.rotation.ten, obj.rotation.y, and obj.rotation.z that correspond rotations about the 10-, y-, and z-axes. The angles are measured in radians. The object is rotated beginning near the ten-axis, and then most the y-centrality, and then nearly the z-axis. (Information technology is possible to change this order.) The value of obj.rotation is not a vector. Instead, information technology belongs to a like type, 3.Euler, and the angles of rotation are called Euler angles.
5.1.3 Object, Geometry, Fabric
A visible object in 3.js is made up of either points, lines, or triangles. An individual object corresponds to an OpenGL primitive such as GL_POINTS, GL_LINES, or GL_TRIANGLES (run across Subsection 3.i.ane). At that place are 5 classes to represent these possibilities: THREE.Points for points, Three.Mesh for triangles, and three classes for lines: THREE.Line, which uses the GL_LINE_STRIP primitive; THREE.LineSegments, which uses the GL_LINES archaic; and THREE.LineLoop, which uses the GL_LINE_LOOP primitive.
A visible object is fabricated up of some geometry plus a cloth that determines the appearance of that geometry. In 3.js, the geometry and material of a visible object are themselves represented by JavaScript classes Three.BufferGeometry and Three.Textile.
An object of type Iii.BufferGeometry can store vertex coordinates and their attributes. (In fact, the vertex coordinates are likewise considered to be an "attribute" of the geometry.) These values must be stored in a grade suitable for use with the OpenGL functions glDrawArrays and glDrawElements (meet Subsection 3.four.2). For JavaScript, this means that they must be stored in typed arrays. A typed array is similar to a normal JavaScript array, except that its length is fixed and information technology can only concord numerical values of a certain blazon. For instance, a Float32Array holds 32-bit floating point numbers, and a UInt16Array holds unsigned sixteen-bit integers. A typed array can exist created with a constructor that specifies the length of the array. For example,
vertexCoords = new Float32Array(300); // Infinite for 300 numbers.
Alternatively, the constructor tin can take an ordinary JavaScript array of numbers as its parameter. This creates a typed array that holds the same numbers. For example,
data = new Float32Array( [ one.3, 7, -two.89, 0, iii, v.5 ] );
In this instance, the length of information is vi, and it contains copies of the numbers from the JavaScript assortment.
Specifying the vertices for a BufferGeometry is a multistep process. You lot need to create a typed array containing the coordinates of the vetices. And so you need to wrap that array inside an object of type THREE.BufferAttribute. Finally, yous can add the attribute to the geometry. Here is an example:
let vertexCoords = new Float32Array([ 0,0,0, 1,0,0, 0,1,0 ]); let vetexAttrib = new THREE.BufferAttribute(vertexCoords, three); let geometry = new Iii.BufferGeometry(); geometry.setAttribute( "position", vertexAttrib );
The second parameter to the BufferGeometry constructor is an integer that tells three.js the number of coordinates of each vertex. Think that a vertex can be specified by 2, 3, or 4 coordinates, and you demand to specify how many numbers are provided in the assortment for each vertex. Turning to the setAttribute() office, a BufferGeometry can have attributes specifying color, normal vectors, and texture coordinates, as well as other custom attributes. The starting time parameter to setAttribute() is the name of the attribute. Here, "position" is the name of the aspect that specifies the coordinates, or position, of the vertices.
Similarly, to specify a color for each vertex, you can put the RGB components of the colors into a Float32Array, and use that to specify a value for the BufferGeometry aspect named "color".
For a specific instance, suppose that we want to represent a primitive of type GL_POINTS, using a iii.js object of type 3.Points. Let'south say we want 10000 points placed at random inside the unit sphere, where each betoken can have its own random colour. Here is some lawmaking that creates the necessary BufferGeometry:
let pointsBuffer = new Float32Array( 30000 ); // 3 numbers per vertex! let colorBuffer = new Float32Array( 30000 ); let i = 0; while ( i < 10000 ) { allow x = 2*Math.random() - 1; let y = 2*Math.random() - 1; permit z = 2*Math.random() - 1; if ( x*ten + y*y + z*z < 1 ) { // only employ points inside the unit of measurement sphere pointsBuffer[iii*i] = x; pointsBuffer[3*i+i] = y; pointsBuffer[3*i+two] = z; colorBuffer[three*i] = 0.25 + 0.75*Math.random(); colorBuffer[3*i+1] = 0.25 + 0.75*Math.random(); colorBuffer[3*i+2] = 0.25 + 0.75*Math.random(); i++; } } let pointsGeom = new THREE.BufferGeometry(); pointsGeom.setAttribute("position", new THREE.BufferAttribute(pointsBuffer,three)); pointsGeom.setAttribute("colour", new THREE.BufferAttribute(colorBuffer,3)); In three.js, to make some geometry into a visible object, nosotros also need an appropriate material. For case, for an object of type THREE.Points, nosotros can utilise a cloth of type THREE.PointsMaterial, which is a subclass of Fabric. The material can specify the color and the size of the points, among other backdrop:
let pointsMat = new THREE.PointsMaterial( { color: "yellow", size: 2, sizeAttenuation: faux } ); The parameter to the constructor is a JavaScript object whose properties are used to initialize the material. With the sizeAttenuation belongings set up to simulated, the size is given in pixels; if information technology is true, then size represents the size in world coordinates and the point is scaled to reverberate altitude from the viewer. If the colour is omitted, a default value of white is used. The default for size is 1 and for sizeAttenuation is true. The parameter to the constructor can be omitted entirely, to use all the defaults. A PointsMaterial is non afflicted by lighting; it but shows the color specified by its color property.
Information technology is as well possible to assign values to properties of the material after the object has been created. For case,
let pointsMat = new Iii.PointsMaterial(); pointsMat.colour = new Iii.Colour("yellow"); pointsMat.size = 2; pointsMat.sizeAttenuation = simulated; Note that the color is set equally a value of type THREE.Color, which is constructed from a string, "xanthous". When the colour property is set in the material constructor, the aforementioned conversion of string to colour is washed automatically.
Once we have the geometry and the fabric, we can utilize them to create the visible object, of type 3.Points, and add it to a scene:
allow sphereOfPoints = new Iii.Points( pointsGeom, pointsMat ); scene.add( sphereOfPoints );
This volition show a cloud of yellow points. But we wanted each point to take its own color! Recall that the colors for the points are stored in the geometry, non in the material. We accept to tell the fabric to apply the colors from the geometry, non the material's ain color property. This is washed by setting the value of the textile property vertexColors to true. And then, we could create the cloth using
let pointsMat = new THREE.PointsMaterial( { color: "white", size: ii, sizeAttenuation: false, vertexColors: true } ); White is used here as the material color because the vertex colors are actually multiplied by the material color, non simply substituted for it.
The following demo shows a betoken cloud. You lot tin can control whether the points are all yellow or are randomly colored. You lot can animate the points, and you can command the size and number of points. Notation that points are rendered equally squares.
The color parameter in the higher up material was specified by the string "yellow". Colors in 3.js tin be represented by values of type THREE.Colour. The course THREE.Color represents an RGB color. A Colour object c has properties c.r, c.g, and c.b giving the ruby-red, bluish, and dark-green color components as floating indicate numbers in the range from 0.0 to one.0. Annotation that there is no alpha component; three.js handles transparency separately from colour.
There are several ways to construct a Three.Color object. The constructor tin can take three parameters giving the RGB components every bit real numbers in the range 0.0 to 1.0. Information technology can have a single cord parameter giving the colour equally a CSS colour string, like those used in the second canvas graphics API; examples include "white", "red", "rgb(255,0,0)", and "#FF0000". Or the color constructor tin can take a unmarried integer parameter in which each color component is given as an eight-bit field in the integer. Ordinarily, an integer that is used to stand for a color in this manner is written as a hexadecimal literal, beginning with "0x". Examples include 0xff0000 for cherry, 0x00ff00 for green, 0x0000ff for blue, and 0x007050 for a nighttime bluish-green. Here are some examples of using color constructors:
allow c1 = new 3.Color("skyblue"); let c2 = new Iii.Colour(i,1,0); // xanthous allow c3 = new THREE.Color(0x98fb98); // pale green In many contexts, such as the Three.Points constructor, three.js will have a string or integer where a colour is required; the cord or integer volition be fed through the Color constructor. As another case, a WebGLRenderer object has a "articulate color" property that is used as the background color when the renderer renders a scene. This property could exist set using whatsoever of the following commands:
renderer.setClearColor( new THREE.Colour(0.half-dozen, 0.4, 0.i) ); renderer.setClearColor( "darkgray" ); renderer.setClearColor( 0x99BBEE );
Turning next to lines, an object of type THREE.Line represents a a line strip—what would be a primitive of the type chosen GL_LINE_STRIP in OpenGL. To go the same strip of connected line segments, plus a line back to the starting vertex, we can utilize an object of blazon THREE.LineLoop. For the outline of a triangle, for case, we could provide a BufferGeometry belongings coordinates for three points and utilise a LineLoop.
We will also need a material. For lines, the material can exist represented by an object of type THREE.LineBasicMaterial. As usual, the parameter for the constructor is a JavaScript object, whose properties can include color and linewidth. For example:
permit lineMat = new THREE.LineBasicMaterial( { color: 0xA000A0, // purple; the default is white linewidth: ii // 2 pixels; the default is 1 } ); (The 3.js documentation says that the linewidth property might not exist respected. Curiously, on my computer, it was respected by a WebGL1Renderer but non by a WebGLRenderer.)
Every bit with points, it is possible to specify a different color for each purpose past adding a "color" attribute to the geometry and setting the value of the vertexColors cloth property to true. Here is a complete example that makes a triangle with vertices colored cherry-red, light-green, and blue:
let positionBuffer = new Float32Array([ -2, -2, // Coordinates for first vertex. two, -ii, // Coordinates for second vertex. 0, 2 // Coordinates for third vertex. ]); let colorBuffer = new Float32Array([ ane, 0, 0, // Color for showtime vertex (red). 0, 1, 0, // Color for second vertex (dark-green). 0, 0, 1 // Color for third vertex (blueish). ]); allow lineGeometry = new Iii.BufferGeometry(); lineGeometry.setAttribute( "position", new 3.BufferAttribute(positionBuffer,two) ); lineGeometry.setAttribute( "colour", new THREE.BufferAttribute(colorBuffer,3) ); let lineMaterial = new Three.LineBasicMaterial( { linewidth: 3, vertexColors: true } ); permit triangle = new Iii.LineLoop( lineGeometry, lineMaterial ); scene.add(triangle); This produces the paradigm:
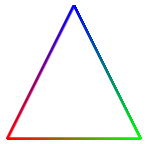
The "Basic" in LineBasicMaterial indicates that this material uses basic colors that do not require lighting to exist visible and are not affected by lighting. This is mostly what you desire for lines.
A mesh object in three.js corresponds to the OpenGL primitive GL_TRIANGLES. The geometry object for a mesh must specify which vertices are part of which triangles. We volition come across how to exercise that in the next section. However, three.js comes with classes to stand for common mesh geometries, such equally a sphere, a cylinder, and a torus. For these built-in classes, you just need to call a constructor to create the appropriate geometry. For instance, the class THREE.CylinderGeometry represents the geometry for a cylinder, and its constructor takes the form
new Iii.CylinderGeometry(radiusTop, radiusBottom, pinnacle, radiusSegments, heightSegments, openEnded, thetaStart, thetaLength)
The geometry created by this constructor represents an approximation for a cylinder that has its axis lying forth the y-centrality. Information technology extends from from −height/2 to height/2 along that centrality. The radius of its round pinnacle is radiusTop and of its bottom is radiusBottom. The two radii don't accept to be the aforementioned; when the are unlike, yous go a truncated cone rather than a cylinder as such. Using a value of zippo for radiusTop makes an actual cone. The parameters radiusSegments and heightSegments give the number of subdivisions around the circumference of the cylinder and along its length respectively—what are called slices and stacks in the GLUT library for OpenGL. The parameter openEnded is a boolean value that indicates whether the peak and bottom of the cylinder are to be drawn; use the value truthful to get an open-ended tube. Finally, the last ii parameters allow y'all to make a partial cylinder. Their values are given as angles, measured in radians, about the y-axis. Only the role of the cylinder beginning at thetaStart and ending at thetaStart plus thetaLength is rendered. For example, if thetaLength is Math.PI, you will get a one-half-cylinder.
The large number of parameters to the constructor gives a lot of flexibility. The parameters are all optional. The default value for each of the outset three parameters is ane. The default for radiusSegments is 8, which gives a poor approximation for a smooth cylinder. Leaving out the last three parameters will give a complete cylinder, closed at both ends.
Other standard mesh geometries are similar. Here are some constructors, listing all parameters (but continue in heed that most of the parameters are optional):
new Iii.BoxGeometry(width, superlative, depth, widthSegments, heightSegments, depthSegments) new THREE.PlaneGeometry(width, height, widthSegments, heightSegments) new THREE.RingGeometry(innerRadius, outerRadius, thetaSegments, phiSegments, thetaStart, thetaLength) new 3.ConeGeometry(radiusBottom, height, radiusSegments, heightSegments, openEnded, thetaStart, thetaLength) new THREE.SphereGeometry(radius, widthSegments, heightSegments, phiStart, phiLength, thetaStart, thetaLength) new 3.TorusGeometry(radius, tube, radialSegments, tubularSegments, arc)
The class BoxGeometry represents the geometry of a rectangular box centered at the origin. Its constructor has iii parameters to give the size of the box in each direction; their default value is 1. The last iii parameters give the number of subdivisions in each direction, with a default of one; values greater than i will cause the faces of the box to be subdivided into smaller triangles.
The class PlaneGeometry represents the geometry of a rectangle lying in the xy-airplane, centered at the origin. Its parameters are similar to those for a cube. A RingGeometry represents an annulus, that is, a deejay with a smaller disk removed from its center. The ring lies in the xy-airplane, with its center at the origin. Yous should always specify the inner and outer radii of the ring.
The constructor for ConeGeometry has exactly the same form and upshot as the constructor for CylinderGeometry, with the radiusTop set to aught. That is, it constructs a cone with axis forth the y-centrality and centered at the origin.
For SphereGeometry, all parameters are optional. The constructor creates a sphere centered at the origin, with axis along the y-centrality. The commencement parameter, which gives the radius of the sphere, has a default of 1. The next ii parameters give the numbers of slices and stacks, with default values 32 and 16. The final 4 parameters allow you to brand a slice of a sphere; the default values requite a complete sphere. The four parameters are angles measured in radians. phiStart and phiLength are measured in angles around the equator and give the extent in longitude of the spherical shell that is generated. For example,
new Iii.SphereGeometry( 5, 32, 16, 0, Math.PI )
creates the geometry for the "western hemisphere" of a sphere. The last two parameters are angles measured along a line of latitude from the northward pole of the sphere to the south pole. For case, to go the sphere's "northern hemisphere":
new Iii.SphereGeometry( five, 32, sixteen, 0, 2*Math.PI, 0, Math.PI/two )
For TorusGeometry, the constructor creates a torus lying in the xy-plane, centered at the origin, with the z-centrality passing through its pigsty. The parameter radius is the distance from the center of the torus to the center of the torus'southward tube, while tube is the radius of the tube. The side by side two parameters give the number of subdivisions in each management. The last parameter, arc, allows you to brand only function of a torus. It is an bending between 0 and 2*Math.PI, measured along the circumvolve at the center of the tube.
At that place are too geometry classes representing the regular polyhedra: THREE.TetrahedronGeometry, Three.OctahedronGeometry, THREE.DodecahedronGeometry, and THREE.IcosahedronGeometry. (For a cube use a BoxGeometry.) The constructors for these four classes take two parameters. The first specifies the size of the polyedron, with a default of 1. The size is given as the radius of the sphere that contains the polyhedron. The 2d parameter is an integer called detail. The default value, 0, gives the actual regular polyhedron. Larger values add detail by adding boosted faces. As the particular increases, the polyhedron becomes a better approximation for a sphere. This is easier to understand with an illustration:

The epitome shows four mesh objects that use icosahedral geometries with item parameter equal to 0, i, ii, and three.
To create a mesh object, you need a material as well as a geometry. In that location are several kinds of cloth suitable for mesh objects, including THREE.MeshBasicMaterial, Iii.MeshLambertMaterial, and THREE.MeshPhongMaterial. (In that location are also 2 newer mesh materials, THREE.MeshStandardMaterial and Three.MeshPhysicalMaterial, that implement techniques associated with physically based rendering, an approach to improved rendering that has get popular. However, I will not cover them here.)
A MeshBasicMaterial represents a color that is not affected past lighting; it looks the same whether or not in that location are lights in the scene, and it is not shaded, giving it a apartment rather than 3D appearance. The other two classes represent materials that demand to exist lit to be seen. They implement models of lighting known every bit Lambert shading and Phong shading. The major difference is that MeshPhongMaterial has a specular color but MeshLambertMaterial does not. Both can have diffuse and emissive colors. For all three material classes, the constructor has one parameter, a JavaScript object that specifies values for properties of the fabric. For example:
let mat = new THREE.MeshPhongMaterial( { color: 0xbbbb00, // reflectivity for diffuse and ambience light emissive: 0, // emission color; this is the default (black) specular: 0x070707, // reflectivity for specular lite shininess: 50 // controls size of specular highlights } ); This case shows the four colour parameters for a Phong material. The parameters have the same meaning as the five cloth backdrop in OpenGL (Subsection iv.i.1). A Lambert material lacks specular and shininess, and a basic mesh material has just the colour parameter.
There are a few other fabric properties that you might need to set in the constructor. Except for flatShading, these employ to all three kinds of mesh material:
- vertexColors — a boolean holding that can be set to truthful to employ vertex colors from the geometry. The default is imitation.
- wireframe — a boolean value that indicates whether the mesh should be drawn equally a wireframe model, showing simply the outlines of its faces. The default is false. A true value works best with MeshBasicMaterial.
- wireframeLinewidth — the width of the lines used to draw the wireframe, in pixels. The default is 1. (Non-default values might not be respected.)
- visible — a boolean value that controls whether the object on which it is used is rendered or not, with a default of true.
- side — has value Iii.FrontSide, Iii.BackSide, or THREE.DoubleSide, with the default being Iii.FrontSide. This determines whether faces of the mesh are drawn or not, depending on which side of the face up is visible. With the default value, Iii.FrontSide, a confront is fatigued only if it is being viewed from the front. THREE.DoubleSide volition draw it whether it is viewed from the front end or from the back, and 3.Backside only if it is viewed from the dorsum. For closed objects, such as a cube or a complete sphere, the default value makes sense, at least as long as the viewer is exterior of the object. For a plane, an open tube, or a fractional sphere, the value should be set to THREE.DoubleSide. Otherwise, parts of the object that should exist in view won't exist drawn.
- flatShading — a boolean value, with the default being imitation. This works just for MeshPhongMaterial. For an object that is supposed to look "faceted," with flat sides, it is important to fix this property to true. That would exist the example, for instance, for a cube or for a cylinder with a small number of sides.
Equally an case, let's make a shiny, blue-green, open up, 5-sided tube with flat sides:
allow mat = new THREE.MeshPhongMaterial( { color: 0x0088aa, specular: 0x003344, shininess: 100, flatShading: true, // for flat-looking sides side: THREE.DoubleSide // for drawing the inside of the tube } ); let geom = new THREE.CylinderGeometry(three,3,10,5,1,truthful); let obj = new THREE.Mesh(geom,mat); scene.add(obj); You can use the post-obit demo to view several three.js mesh objects, using a multifariousness of geometries and materials. Drag your mouse on the object to rotate information technology. You tin besides explore the level of item for the regular polyhedron geometries.
The demo can bear witness a wireframe version of an object overlaid on a solid version. In three.js, the wireframe and solid versions are really two objects that utilize the aforementioned geometry but different materials. Cartoon two objects at exactly the same depth can be a problem for the depth test. You might remember from Subsection 3.4.ane that OpenGL uses polygon offset to solve the problem. In 3.js, yous tin can apply polygon start to a material. In the demos, this is done for the solid materials that are shown at the aforementioned fourth dimension equally wireframe materials. For example,
mat = new Three.MeshLambertMaterial({ polygonOffset: true, polygonOffsetUnits: 1, polygonOffsetFactor: 1, color: "yellow", side: THREE.DoubleSide }); The settings shown here for polygonOffset, polygonOffsetUnits, and polygonOffsetFactor volition increase the depth of the object that uses this material slightly so that it doesn't interfere with the wireframe version of the same object.
Ane final note: Y'all don't always need to brand new materials and geometries to make new objects. You can reuse the same materials and geometries in multiple objects.
5.1.iv Lights
Compared to geometries and materials, lights are easy! Iii.js has several classes to represent lights. Light classes are subclasses of 3.Object3D. A low-cal object can be added to a scene and volition then illuminate objects in the scene. We'll expect at directional lights, indicate lights, ambience lights, and spotlights.
The class 3.DirectionalLight represents light that shines in parallel rays from a given direction, like the light from the sun. The position property of a directional light gives the management from which the calorie-free shines. (This is the aforementioned position holding, of type Vector3, that all scene graph objects take, just the meaning is dissimilar for directional lights.) Note that the light shines from the given position towards the origin. The default position is the vector (0,one,0), which gives a calorie-free shining downward the y-centrality. The constructor for this class has two parameters:
new THREE.DirectionalLight( colour, intensity )
where color specifies the color of the lite, given every bit a THREE.Color object, or as a hexadecimal integer, or as a CSS color string. Lights do non have separate diffuse and specular colors, as they do in OpenGL. The intensity is a non-negative number that controls the effulgence of the calorie-free, with larger values making the light brighter. A light with intensity zero gives no light at all. The parameters are optional. The default for colour is white (0xffffff) and for intensity is 1. The intensity tin exist greater than i, but values less than 1 are usually preferable, to avoid having as well much illumination in the scene.
Suppose that we have a camera on the positive z-axis, looking towards the origin, and we would like a light that shines in the aforementioned direction that the photographic camera is looking. We can utilise a directional lite whose position is on the positive z-axis:
let light = new Iii.DirectionalLight(); // default white light light.position.set( 0, 0, one ); scene.add(light);
The form Three.PointLight represents a lite that shines in all directions from a point. The location of the signal is given by the light'southward position property. The constructor has three optional parameters:
new THREE.PointLight( color, intensity, cutoff )
The first two parameters are the same as for a directional low-cal, with the same defaults. The cutoff is a non-negative number. If the value is zero—which is the default—then the illumination from the light extends to infinity, and intensity does not decrease with distance. While this is not physically realistic, it mostly works well in practice. If cutoff is greater than nada, and then the intensity falls from a maximum value at the calorie-free's position down to an intensity of zero at a altitude of cutoff from the lite; the low-cal has no effect on objects that are at a altitude greater than cutoff. This falloff of calorie-free intensity with distance is referred to equally attenuation of the light source.
A third type of low-cal is THREE.AmbientLight. This course exists to add ambient light to a scene. An ambience low-cal has simply a color:
new THREE.AmbientLight( color )
Adding an ambient light object to a scene adds ambience light of the specified color to the scene. The colour components of an ambient low-cal should be rather minor to avoid washing out colors of objects.
For instance, suppose that we would similar a yellowish signal light at (10,30,fifteen) whose illumination falls off with distance from that signal, out to a distance of 100 units. We also want to add a bit of xanthous ambient lite to the scene:
permit light = new 3.PointLight( 0xffffcc, ane, 100 ); light.position.set( ten, 30, 15 ); scene.add together(light); scene.add( new Three.AmbientLight(0x111100) );
The fourth type of calorie-free, Three.SpotLight, is something new for us. An object of that blazon represents a spotlight, which is similar to a point light, except that instead of shining in all directions, a spotlight simply produces a cone of low-cal. The vertex of the cone is located at the position of the low-cal. By default, the centrality of the cone points from that location towards the origin (so unless you lot change the direction of the centrality, you should movement the position of the low-cal away from the origin). The constructor adds two parameters to those for a indicate calorie-free:
new THREE.SpotLight( colour, intensity, cutoff, coneAngle, exponent )
The coneAngle is a number between 0 and Math.PI/2 that determines the size of the cone of light. It is the angle between the axis of the cone and the side of the cone. The default value is Math.PI/three. The exponent is a non-negative number that determines how fast the intensity of the light decreases every bit y'all movement from the axis of the cone toward the side. The default value, ten, gives a reasonable effect. An exponent of cypher gives no falloff at all, and then that objects at all distances from the axis are evenly illuminated.
The technique for setting the direction of a three.js spotlight is a little odd, but information technology does make it easy to command the direction. An object spot of blazon SpotLight has a belongings named spot.target. The target is a scene graph node. The cone of low-cal from the spotlight is pointed in the direction from spotlight'due south position towards the target's position. When a spotlight is first created, its target is a new, empty Object3D, with position at (0,0,0). Even so, yous can set the target to be any object in the scene graph, which will make the spotlight smooth towards that object. For three.js to calculate the spotlight management, a target whose position is anything other than the origin must really be a node in the scene graph. For example, suppose we want a spotlight located at the betoken (0,0,5) and pointed towards the point (2,ii,0):
spotlight = new Iii.SpotLight(); spotlight.position.gear up(0,0,5); spotlight.target.position.set up(2,2,0); scene.add together(spotlight); scene.add(spotlight.target);
The interaction of spotlights with material illustrates an important departure between Phong and Lambert shading. With a MeshLambertMaterial, the lighting equation is applied at the vertices of a primitive, and the vertex colors computed by that equation are so interpolated to calculate colors for the pixels in the primitive. With MeshPhongMaterial, on the other paw, the lighting equation is applied at each individual pixel. The following analogy shows what can happen when nosotros shine a spotlight onto a foursquare that was created using THREE.PlaneGeometry:

For the ii squares on the left, the square was not subdivided; it is fabricated up of two triangular faces. The foursquare at the far left, which uses Phong shading, shows the expected spotlight effect. The spotlight is pointed at the center of the square. Note how the illumination falls off with distance from the center. When I used the same square and spotlight with Lambert shading in the 2d motion picture, I got no illumination at all! The vertices of the the square prevarication outside the cone of light from the spotlight. When the lighting equation is applied, the vertices are black, and the blackness color of the vertices is and then applied to all the pixels in the foursquare.
For the third and quaternary squares in the analogy, aeroplane geometries with horizontal and vertical subdivisions were used with Lambert shading. In the third picture, the square is divided into three subdivisions in each direction, giving eighteen triangles, and the lighting equation is practical only at the vertices of those triangles. The consequence is notwithstanding a very poor approximation for the correct illumination. In the fourth square, with 10 subdivisions in each direction, the approximation is better but yet not perfect.
The upshot is, if you want an object to be properly illuminated by a spotlight, utilize a MeshPhongMaterial on the object, even if it has no specular reflection. A MeshLambertMaterial will only give acceptable results if the faces of the object are very small.
five.i.5 A Modeling Example
In the rest of this affiliate, nosotros will go much deeper into three.js, merely you lot already know plenty to build 3D models from bones geometric objects. An example is in the sample program threejs/diskworld-1.html, which shows a very elementary model of a motorcar driving around the edge of a cylindrical base. The car has rotating tires. The diskworld is shown in the flick on the left beneath. The picture on the right shows i of the axles from the car, with a tire on each end.
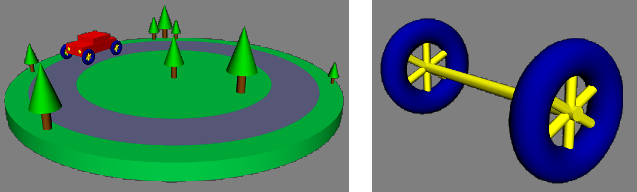
I will discuss some of the code that is used to build these models. If you lot desire to experiment with your ain models, you lot can use the program threejs/modeling-starter.html as a starting point.
To outset with something simple, let'due south look at how to brand a tree from a brown cylinder and a green cone. I use an Object3D to correspond the tree as a whole, so that I can treat information technology every bit a unit. The ii geometric objects are added as children of the Object3D.
let tree = new Three.Object3D(); let trunk = new THREE.Mesh( new THREE.CylinderGeometry(0.2,0.2,1,16,i), new 3.MeshLambertMaterial({ color: 0x885522 }) ); trunk.position.y = 0.5; // move base up to origin let leaves = new 3.Mesh( new THREE.ConeGeometry(.vii,two,xvi,iii), new 3.MeshPhongMaterial({ color: 0x00BB00, specular: 0x002000, shininess: 5 }) ); leaves.position.y = 2; // motility bottom of cone to tiptop of body tree.add together(trunk); tree.add together(leaves); The trunk is a cylinder with height equal to 1. Its centrality lies forth the y-axis, and it is centered at the origin. The plane of the diskworld lies in the xz-plane, so I want to motion the bottom of the trunk onto that plane. This is done by setting the value of trunk.position.y, which represents a translation to be practical to the body. Call back that objects take their own modeling coordinate system. The properties of objects that specify transformations, such as trunk.position, transform the object in that coordinate system. In this example, the body is part of a larger, compound object that represents the whole tree. When the scene is rendered, the body is get-go transformed by its own modeling transformation. It is and then farther transformed by any modeling transformation that is applied to the tree as a whole. (This type of hierarchical modeling was get-go covered in Subsection 2.4.1.)
Once nosotros have a tree object, it can be added to the model that represents the diskworld. In the programme, the model is an object of blazon Object3D named diskworldModel. The model will comprise several copse, but the trees don't accept to be synthetic individually. I can brand boosted copse by cloning the ane that I have already created. For case:
tree.position.ready(-i.5,0,ii); tree.calibration.prepare(0.7,0.7,0.7); diskworldModel.add( tree.clone() ); tree.position.set up(-1,0,5.two); tree.scale.gear up(0.25,0.25,0.25); diskworldModel.add( tree.clone() );
This adds two trees to the model, with dissimilar sizes and positions. When the tree is cloned, the clone gets its own copies of the modeling transformation properties, position and scale. Irresolute the values of those properties in the original tree object does not affect the clone.
Lets turn to a more complicated object, the axle and wheels. I commencement by creating a wheel, using a torus for the tire and using 3 copies of a cylinder for the spokes. In this case, instead of making a new Object3D to hold all the components of the wheel, I add together the cylinders as children of the torus. Recall that whatsoever screen graph node in three.js can have child nodes.
allow bicycle = new THREE.Mesh( // the tire; spokes will be added as children new Three.TorusGeometry(0.75, 0.25, 16, 32), new Iii.MeshLambertMaterial({ colour: 0x0000A0 }) ); let xanthous = new Iii.MeshPhongMaterial({ colour: 0xffff00, specular: 0x101010, shininess: 16 }); let cylinder = new Three.Mesh( // a cylinder with top i and bore ane new Iii.CylinderGeometry(0.v,0.five,1,32,1), yellow ); cylinder.scale.prepare(0.fifteen,1.ii,0.15); // Make it thin and alpine for use as a spoke. wheel.add( cylinder.clone() ); // Add a copy of the cylinder. cylinder.rotation.z = Math.PI/3; // Rotate information technology for the second spoke. wheel.add( cylinder.clone() ); cylinder.rotation.z = -Math.PI/3; // Rotate it for the third spoke. cycle.add( cylinder.clone() ); In one case I have the wheel model, I can use it along with ane more cylinder to make the axle. For the axle, I use a cylinder lying forth the z-axis. The wheel lies in the xy-plane. Information technology is facing in the right direction, but information technology lies in the center of the beam. To get information technology into its correct position at the cease of the beam, it just has to be translated forth the z-centrality.
axleModel = new Iii.Object3D(); // A model containing two wheels and an beam. cylinder.calibration.gear up(0.2,four.3,0.ii); // Scale the cylinder for use every bit an beam. cylinder.rotation.prepare(Math.PI/2,0,0); // Rotate its centrality onto the z-centrality. axleModel.add together( cylinder ); wheel.position.z = two; // Wheels are positioned at the two ends of the axle. axleModel.add( cycle.clone() ); bike.position.z = -two; axleModel.add together( wheel );
Note that for the second wheel, I add the original wheel model rather than a clone. In that location is no need to brand an extra re-create. With the axleModel in hand, I tin build the car from 2 copies of the axle plus some other components.
The diskworld tin be animated. To implement the animation, properties of the advisable scene graph nodes are modified before each frame of the blitheness is rendered. For example, to brand the wheels on the motorcar rotate, the rotation of each axle about its z-axis is increased in each frame:
carAxle1.rotation.z += 0.05; carAxle2.rotation.z += 0.05;
This changes the modeling transformation that will exist practical to the axles when they are rendered. In its own coordinate system, the central centrality of an beam lies along the z-centrality. The rotation about the z-axis rotates the axle, with its attached tires, about its axis.
For the total details of the sample program, see the source code.
Source: https://math.hws.edu/graphicsbook/c5/s1.html
Posted by: tedderdiecaut.blogspot.com

0 Response to "Should Camera Belong To Renderer Or Scene"
Post a Comment